B 树
B树的的相关知识依赖m路搜索树:
[[m路搜索树]]
定义
一棵 m 阶B_树是一棵 m 路搜索树,它或者是空树,或者是满足下列性质的树:
- 根结点至少有 2 个子女
- 除根结点以外的所有结点 (不包括失败结点)至少有
个子女 - 所有的失败结点都位于同一层。
Note: 失败结点:是当搜索值x不在树中时才能到达的结点
注意:事实上,在B树的每个结点中还包含有一组指针D[m],指向实际对象的存放地址。K[i]与D[i]形成一个索引项(K[i], D[i]),通过K[i]可找到某个对象的存储地址D[i]。
搜索时间分析
B树的搜索时间分为两种情况考虑
- 搜索成功所需的时间:取决于关键码所在的层次
- 搜索不成功所需的时间:取决于树的高度。
插入节点的方法
- B树是从空树起,逐个插入关键码而生成的
- 在B树,每个非失败结点的关键码个数都在
之间。 - 插入在最底层的非失败结点开始。如果在关键码插入后结点中的关键码个数超出了上界 m-1,则结点需要“分裂”,否则可以直接插入
插入时节点分裂的方法
设结点 p 中已经有 m-1 个关键码当再插入一个关键码后结点中的状态为
这时必须把结点 p 分裂成两个结点 p 和 q,它们包含的信息分别为:
- P:
- Q:
此时把中间的节点插入到原来节点p的父节点中,然后递归向上搜索,调整
删除
- 首先需要找到这个关键码所在的结点, 从中删去这个关键码。
- 若该结点不是叶结点, 且被删关键码为
, 则在删去该关键码之后, 应以该结点 所指示子树中的最小关键码 来代替被删关键码 所在的位置 - 然后在叶子节点上删除
在叶子节点上删除有以下几种情况: - 被删关键码所在叶结点同时又是根结点且删除前该结点中关键码个数
,则直接删去该关键码并将修改后的结点写回磁盘。 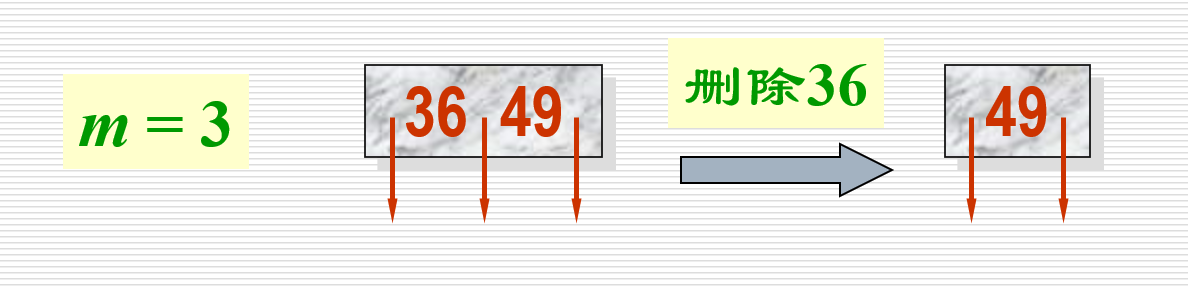
- 被删关键码所在叶结点不是根结点且删除前该结点中关键码个数
, 则直接删去该关键码并将修改后的结点写回磁盘, 删除结束。 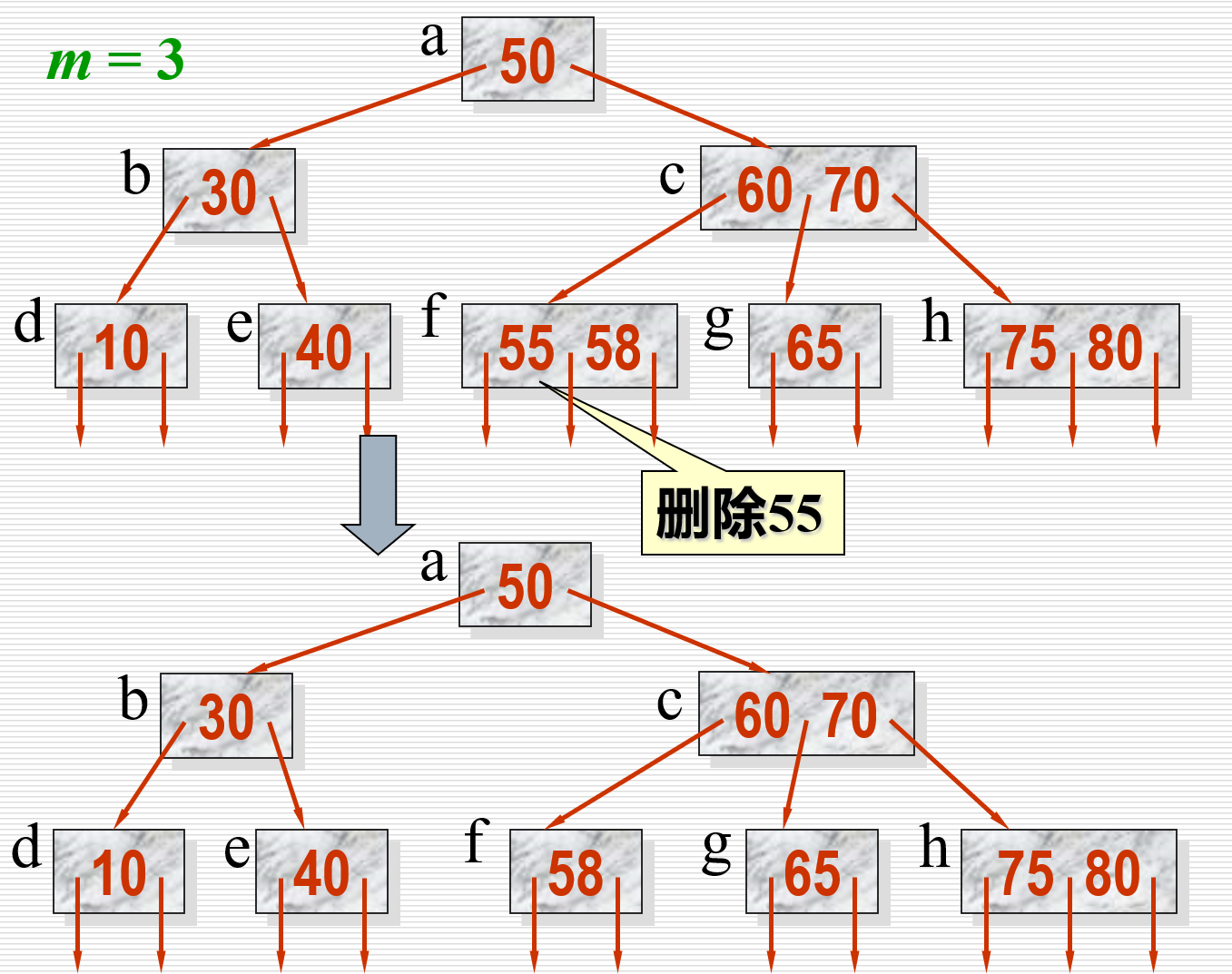
- 被删关键码所在叶结点删除前关键码个数
, 若这时与该结点相邻的右兄弟 (或左兄弟) 结点的关键码个数 ,则可按以下步骤调整该结点、右兄弟 (或左兄弟) 结点以及其双亲结点,以达到新的平衡: - 将这两个节点的共同父结点中刚刚大于 (或小于) 该被删关键码的关键码
下移 - 将右兄弟 (或左兄弟) 结点中的最小 (或最大) 关键码上移到父亲结点的
位置 - 将右兄弟 (或左兄弟) 结点中的最左 (或最右) 子树指针平移到被删关键码所在结点中最后 (或最前) 子树指针位置
- 在右兄弟 (或左兄弟) 结点中,将被移走的关键码和指针位置用剩余的关键码和指针填补、调整。再将结点中的关键码个数减1
如图所示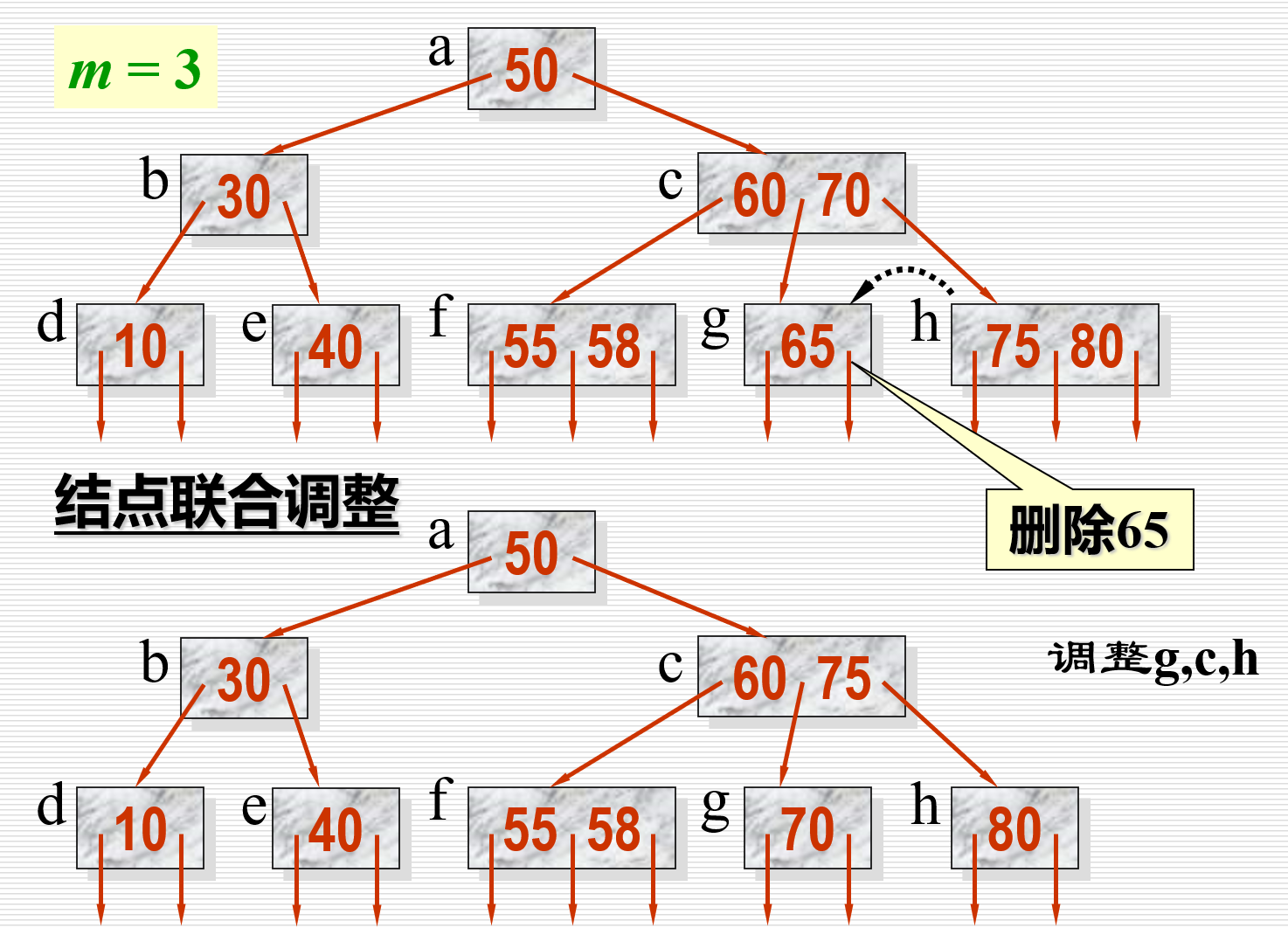
这张图里面也可以选择使用左侧的58来做替换
- 将这两个节点的共同父结点中刚刚大于 (或小于) 该被删关键码的关键码
- 被删关键码所在叶结点删除前关键码个数
, 若这时与该结点相邻的右兄弟 (且左兄弟) 结点的关键码个数 , 则“合并”。 - 假设合并至左兄弟,且其结点地址由双亲结点中的指针
所指,则在删除关键字后,它所在结点中的剩余信息,加上双亲结点中关键字 一起,合并至 所指结点中。 - 假设合并至右兄弟,且其结点地址由双亲结点中的指针
所指,则在删除关键字后,它所在结点中的剩余信息,加上双亲结点中关键字 一起,合并至 所指结点中。
合并至左兄弟的具体方法: - 将双亲结点 P 中相应关键码下移到选定保留的结点(左兄弟)中。若要合并 P 中的子树指针
与 所指的结点, 且保留 所指结点, 则把 P 中的关键码 下移到 所指的结点中。 - 把 P 中子树指针
所指结点中的全部指针和关键码都照搬到 所指结点的后面。删去 所指的结点。 - 在结点 P 中用后面剩余的关键码和指针填补关键码
和指针 。 - 修改结点 P 和选定保留结点的关键码个数。
示例图如下:
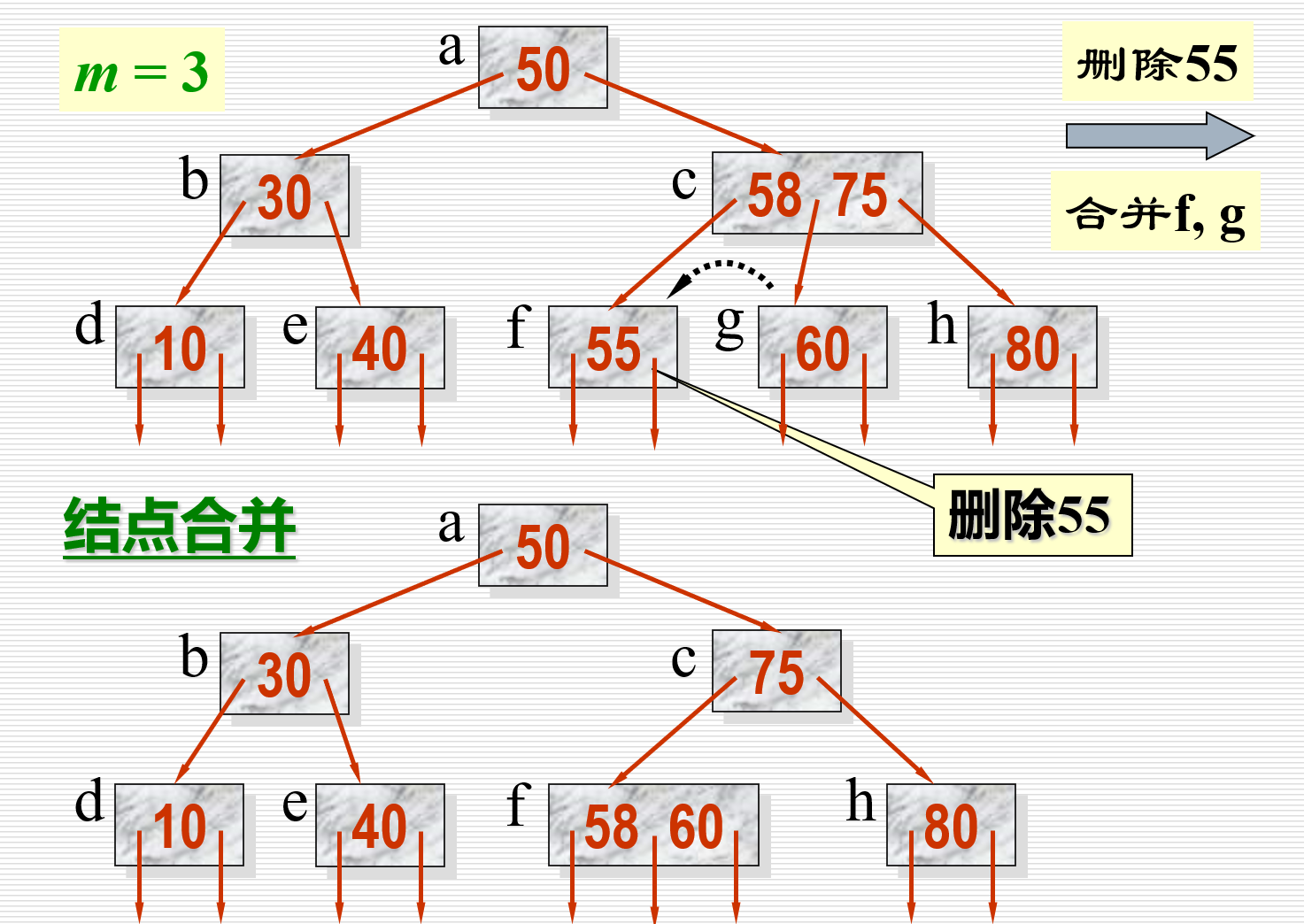
另一侧同理,如下图
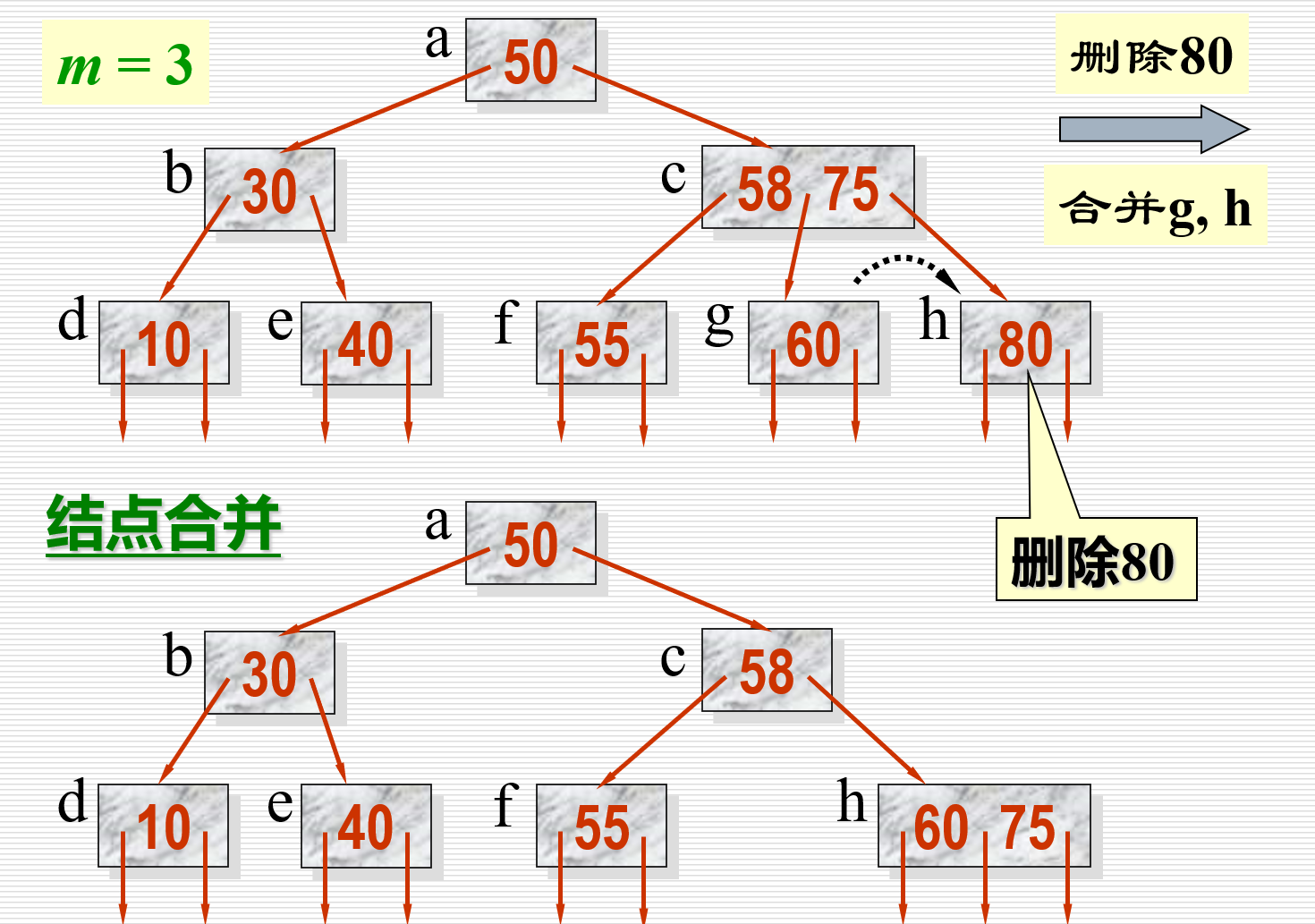
- 假设合并至左兄弟,且其结点地址由双亲结点中的指针
- 合并过程中对父节点的调整:
由于删除过程中,父节点的关键码个数减少了,所以可能仍然需要进行合并:- 若双亲结点是根结点且结点关键码个数减到 0, 则将该双亲结点删去, 合并后保留的结点成为新的根结点; 否则将双亲结点与合并后保留的结点都写回磁盘, 删除处理结束。
- 若双亲结点不是根结点且关键码个数减到
,又要与它自己的兄弟结点合并, 重复上面的合并步骤。
注意,在删除的时候能不进行合并操作就不要进行合并,优先进行替换操作
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
