红黑树学习笔记
Definition
- 节点是红色或者黑色
- 根节点是红色
- 叶子节点是黑色
- 红色节点不能有红色子节点
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点(简称黑高)
ARB and RB
ARB(Almost red-black tree) 和红黑树的区别就是根节点是红色
Black height
The black height of any
和B树的关系
可以把同一层(两个红色节点链接在一个黑色节点后面记为一层)的红色节点和黑色节点放到一起,相当于就是一个2-4 B树
修复的基本操作
红黑树的修复是通过变色、左旋和右旋三种操作组合而成的,关于旋转的操作详见[[AVL#AVL树基本结构]]
插入流程
插入的概略过程:
- 先插入一个结点
- 将插入的结点标记为红色(Black height constraint仍然成立)
- 在保证Black height constraint的情况下,调整颜色和结构,使得Color constraint成立
在插入节点之后,可能RBT的性质被破坏了,此时需要进行修改,一般分为四节点和三节点两种情况
四节点修复
四节点修复只有变色这一种修复方式,具体如下图所示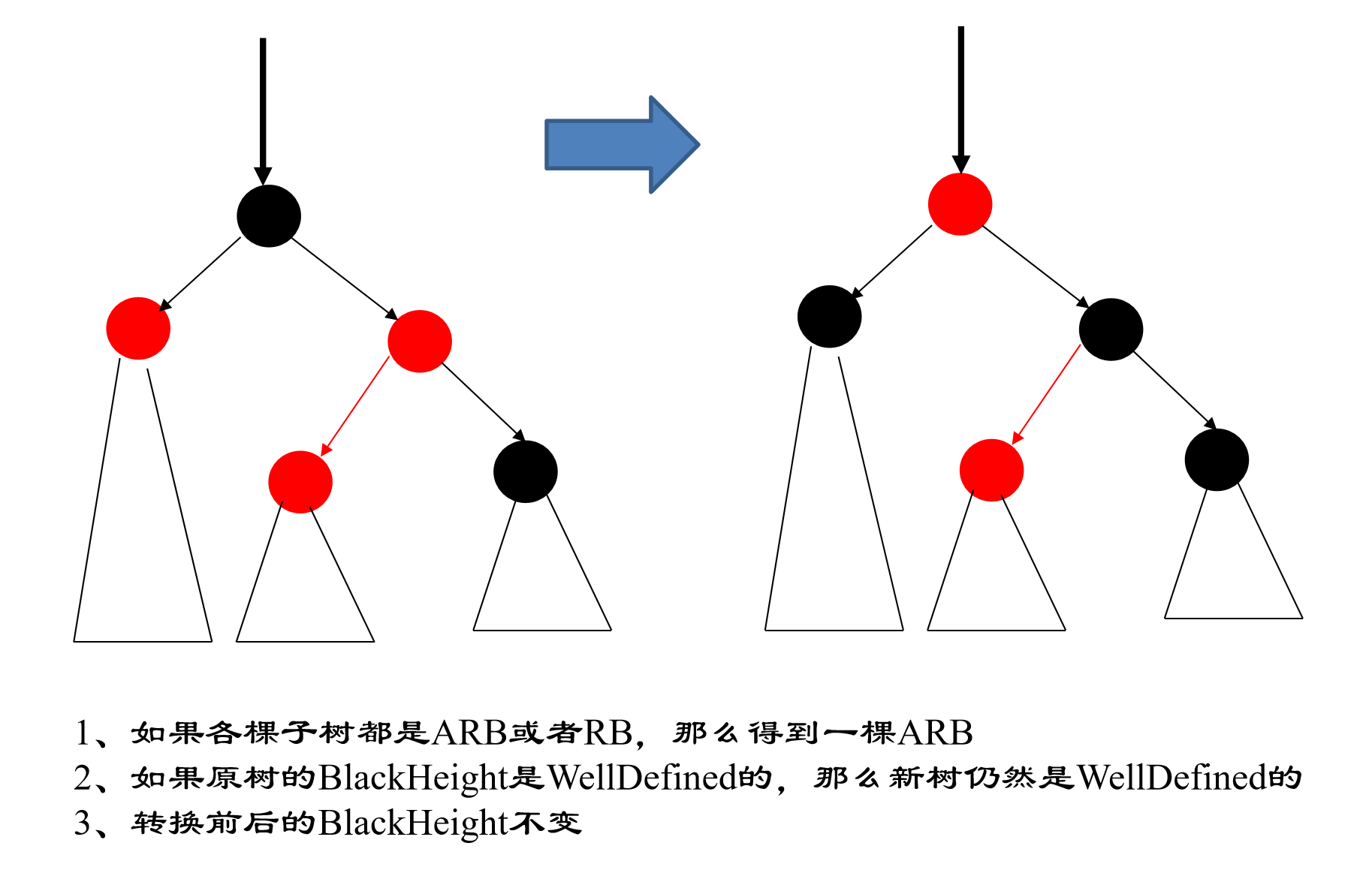
四节点的修复本质上就是上两层的节点变色,后面的不变色。
在这种情况下,通过改变颜色,让子树的颜色约束达成,但是父节点颜色改变,可能把需要修复的红色向根节点方向传递,此时需要递归地向上修复
三节点的情况
三节点的错误情况一共可能有一下四种:
可以发现,三节点不能仅仅通过四节点的变色方法进行修复。
而对于三节点的情况,有以下断言
3-node Critical Clusert满足下面的条件:
1、都具有4个“子树”,且这些“子树”的根结点都是黑色
2、都满足LL < L < LR < M < RL < R < RR
对应的处理方法如下:
Case A
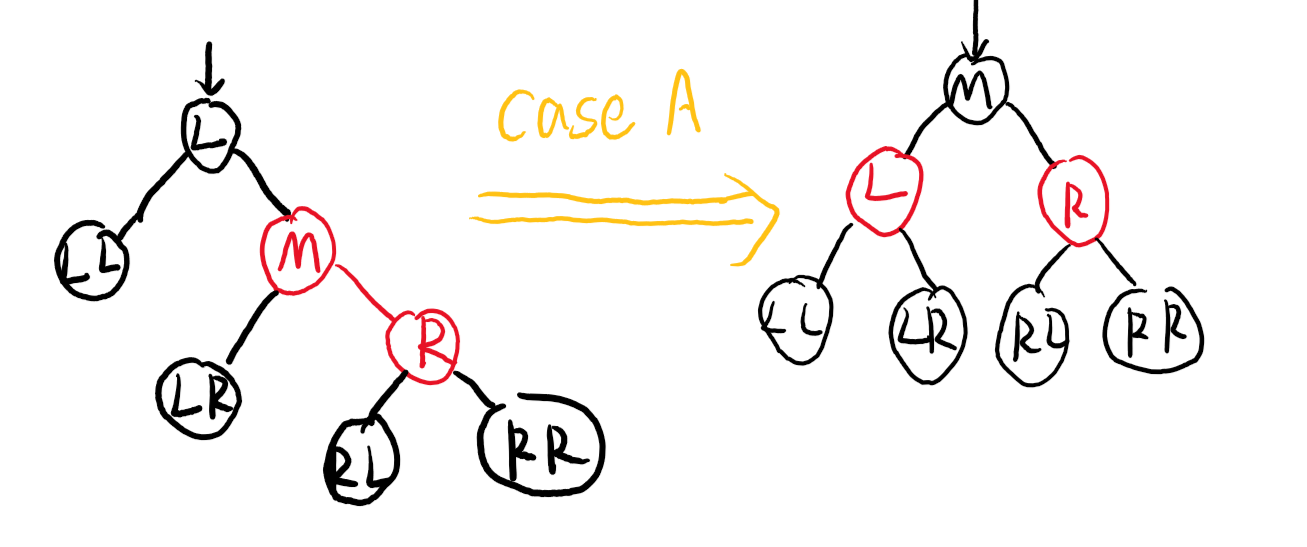
Case B
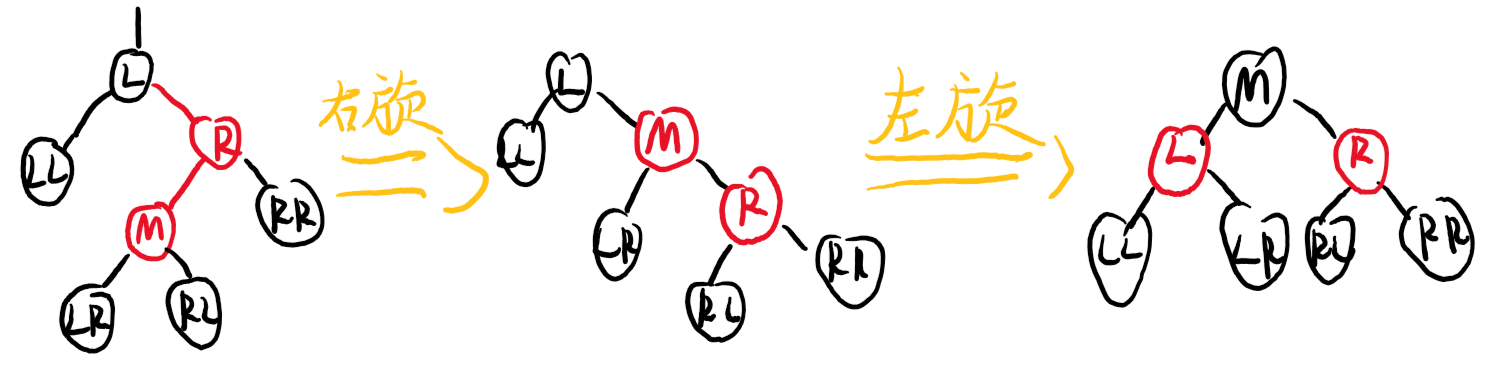
Case C
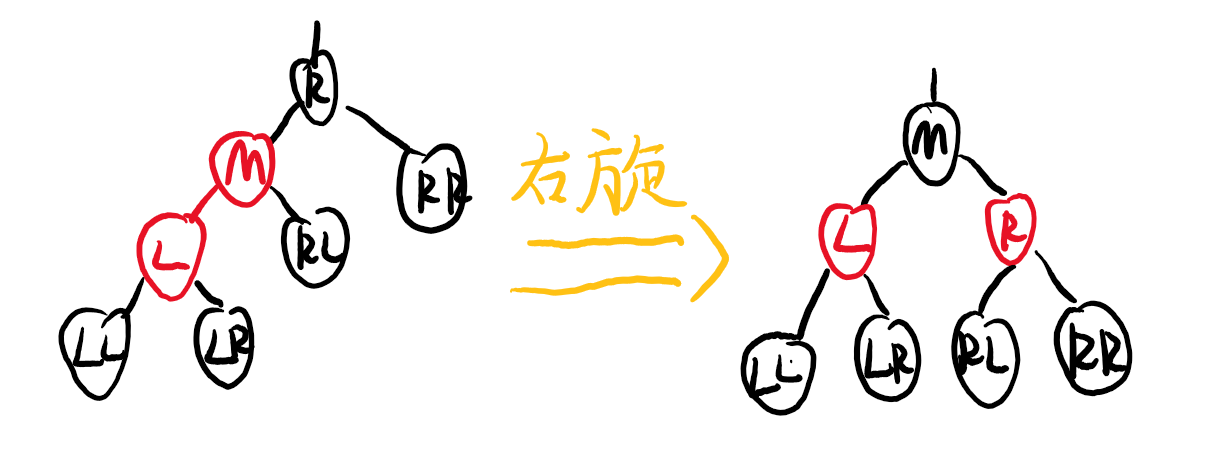
Case D

经过观察不难发现,四种情况下搜不会把不满足的性质继续向上传递,所以至多一次三节点调整就可以使树重新满足性质
其实红黑树在平衡树的角度看,插入的调整和AVL是一致的,只是不需要调整平衡因子,只需要改变颜色就行了。不过也可以在B树的角度看,每个旋转就是B树里面的分裂和合并。
TODO
完成插入全流程和删除操作
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
