Dual cone

Definition

Dual cone of a given cone K is

Property

  • is convex even if is not.
  • if and only if is the normal of a hyperplane that support at the origin
    换句话说，只有当向量 是锥 的在顶点处的一个支撑超平面的法向量的时候，才会属于它的对偶锥，如图

    形象一些理解的话，就是想象一个原来的锥  ，然后对偶锥就是对两条边界射线做垂线，这两条垂线内部就是对偶锥。
  • implies
  • if has nonempty interior, then is pointed

Dual Generalized Inequalities

![[Cone#Generalized inequality]]
if and only if for all

Proof

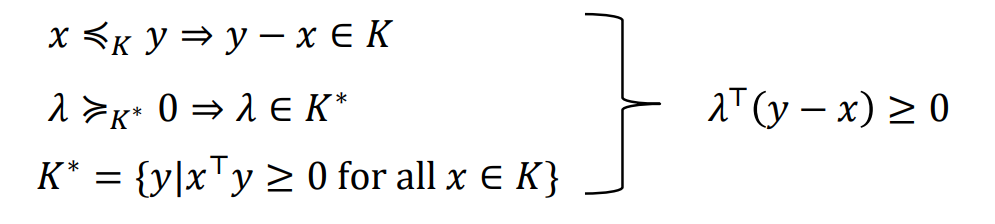
Dual Characterization of Minimum Element

x is the minimum element of , with respect to the generalized inequality if and only if for all , x is the unique minimizer of over

Proof

The proof depends on supporting hyperplane.

If for any , we get the hyperplane is strict supporting hyperplane to the given set at point .

Dual Characterization of Minimal Element

If and x minimizes over then is minimal.

Give an example below: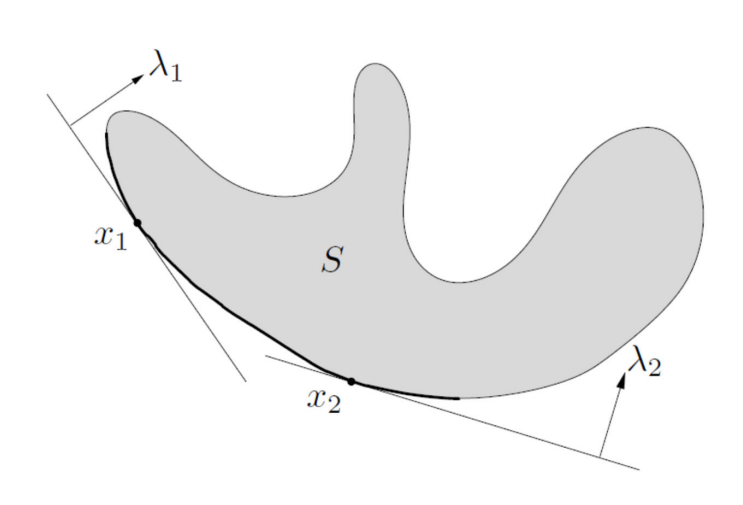
An example of minimal element