PRG and PRF
PRG
Background
提出的背景是生成真随机函数的速度太慢了,如果通过CPU温度来生成真随机,那么不能满足加密的速度要求,进而提出一种伪随机方法,来通过比较短的随机种子生成更长的随机串
Definition
定义一个多项式 PRG 的:
- 拓展性(Expansion):
- 对于任意PPT时间范围内的区分器
,都有一个可忽略函数 使得
其中的均匀且随机,是真随机,而 是独立采样的,注意区分器是看不到 的,也不能看到 具体是什么 但是你构造反证的时候,是能够知道G的特征的,并且需要依据G的特殊性构造 这不是扯淡,因为你只需要证明存在一个D就可以了 ——By Danny
这里的实验分两种情况:
- 如果是走前半边,那么就是随机等可能从
里面采样出一个 出来,然后传给 输出一个数给判别器。 - 后半边是随机从
里面采样出一个 ,传给判别器 。
判别器
注意:
- PRG的算法本身不是随机的
- 使用PRG算法生成的随机数的分布依赖于传入种子的分布,本身不一定是均匀的
- 存在
时间复杂度的破解算法
伪随机的本质就是通过算法
,将短的种子的随机性拓展到更长的一串字符上
Usage
可以通过伪随机数生成器构造一个能够防范唯密文攻击的定长加密算法
- Gen: 在输入参数
的时候,独立地采样 然后输出 为key - Enc: 在获得 k 和明文
之后,输出密文: - Dec: 在获得
和密文 之后,明文可写为:
接下来给出该方法在满足伪随机条件的时候是可以防范唯密文攻击的
Proof
规约证明法
即通过构造,说明该情况和之前的某种定义矛盾,如下图所示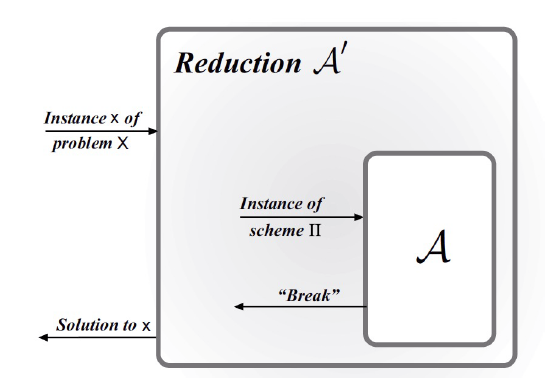
具体证明
具体实验的定义参考 ![[Computational security, CPA security and CCA security#The Adeversarial indistinguishable experiment (计算安全实验)]]
考虑进行规约证明,即证明如果可以构造出一种攻击者,那么会破坏伪随机的定义
构造出另一种加密模式
根据前面的证明,
如果此时的存在攻击者
其中的
那么可以基于这个
Simulate the distinguishable experiment with
with and respectively, use this ciphertext distinguisher as our required
pseudo-randomness/randomness distinguisher .
Ifwins, output 1.
从教材上看,区分器
更具体地说:
接受一个可能是 也可能是 的传入 key调用前文给出的攻击者 , 向区分器 输出两个明文 等概率选择 ,向 输入 和 key,并获得的输出 - 如果
,则认为是伪随机,否则认为是真随机
那么此时有
$$
\mathtt{Pr}[D(G(s)) = 1] = \mathtt{Pr}[A’ \text{wins} \mathtt{PrivK}{\mathcal{A’}\Pi}^{eav}] = \mathtt{Pr}[\mathtt{PrivK}{\mathcal{A’}\Pi}^{eav}]
$$
Q:为啥上面这个是对的呢?
Answer by Danny:分类讨论,如果给的是真随机函数,那么三个概率都是如果如果给 的是伪随机数 ,那么 判断正确等价于 认为 ,那么 认为 当且仅当 猜对了
Q:猜对 的情况下 会认为 是定义,但是这不代表 判断成功的概率和 获胜的概率一样啊
A: 想岔了吧,就是相等的。这个是根据定义相等,通过和 的定义相等的
分析以上过程,可以发现,区分器
而
PRF
如果只使用PRG,那么在遇到选择明文攻击的时候,可以通过简单的查询,获得PRG的相关信息,那么加密就是不可靠的了,为了进一步提升安全性,满足CPA安全,提出了PRF
PRF可以看做是PRG的升级版本,PRF在每一个 key 给定的情况下,就可以当做一个PRG使用。
Definition
- 一个带
key的函数key和一个长度为
特别地,如果length-preserving的 - 如果有一个多项式时间的算法可以计算出
- 如果
key是独立随机地选择的,那么函数 - 如果随机采样了
key之后每一个
基于 PRF 构造满足CPA安全的加密方式
加密流程
假设
- Gen: 在输入
- Enc: 在输入
key和输入 - Dec: 在输入
key和密文对
合理性证明
CPA 安全实验参考 ![[Computational security, CPA security and CCA security#CPA安全实验]]
和上面的 PRG 的证明非常类似,构造一个
首先,可以证明没有PPT时间内的攻击者可以在这种情况下分辨 PRF 和真随机函数,即
$$
\left|\mathtt{Pr}[\mathtt{Priv}{\mathcal{A},\Pi}^{cpa} = 1] - \mathtt{Pr}[\mathtt{Priv}{\mathcal{A},\hat{\Pi}}^{cpa} = 1]\right|
\leq \mathtt{negl}(n)
$$
说明方法就是上面PRG的证明方案
然后,证明没有PPT时间内的攻击者可以在不可忽视的概率下赢得 CPA安全实验,即:
其中的
这几乎是显然的,因为一个真的从
$$
\mathtt{Pr}[\mathtt{Priv}{\mathcal{A},\hat{\Pi}}^{cpa} = 1] \
=\mathtt{Pr}[\mathtt{Priv}{\mathcal{A},\hat{\Pi}}^{cpa} = 1|\text{no require maches}] \cdot \mathtt{Pr}[\text{no require maches}] + \mathtt{Pr}[\mathtt{Priv}_{\mathcal{A},\hat{\Pi}}^{cpa} = 1 | \text{has require maches}] \cdot \mathtt{Pr}[\text{has require maches}]\
\leq \frac{1}{2} \cdot 1 + 1 \cdot \frac{q(n)}{2^n}
$$
将以上两点合并到一起看,不难发现
基于PRF 构造 PRG
构造
合理性证明
假设存在一个多项式时间内的区分器
构造一个区分器
所以此处的
