Finite Markov Decision
马尔科夫模型中与环境交互的定义
Agent做出动作 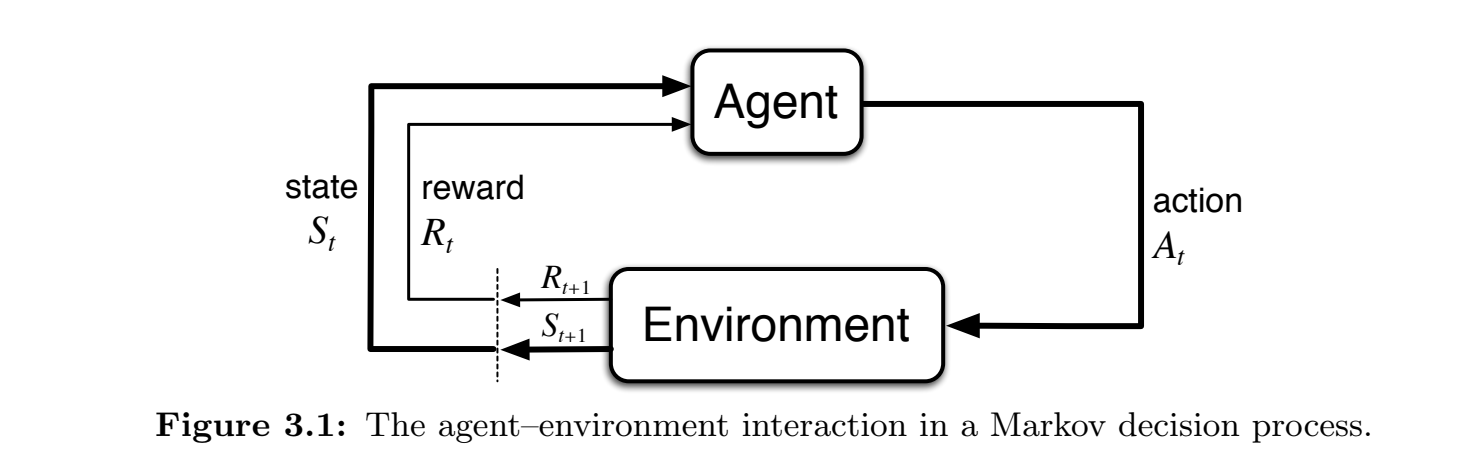
有限马尔科夫决策过程的规定
在有限马尔科夫决策过程中,所有的 states,actions,rewards 的集合都是有限的,而随机变量 state和action 的离散的概率分布,即只有上一次的状态和选择会影响当前的状态和奖励。
转移函数
定义转移函数
转移函数
该函数有如下的性质:
奖励期望的定义
在MDP中,奖励的期望被定义为
如何确定合理的奖励
这里的奖励应该设置成为学习的额最终目标,例如如果是训练围棋,那么奖励应该设置为获得胜利,只有获得胜利的时候才会得到1的奖励,不能设置为吃子,这样训练的结果会变成一个以吃子为目标而不是以获胜为目标的算法。
两种不同的任务类型
可以分成 episode 的
如果 agent 与 environment 的交互可以自然地分成多个 episode 那么就可以得到一个终结状态,记为
就可以求出对应的期望了
持续性任务
如果没有终结时刻,即
这个式子是可以证明收敛的:
假设这里的
中最大的是 那么有:
这里的参数
这里选择给每个
reward加上一个权是考虑如果一个奖励越晚到达,那么它在当前的情况下的重要性就越低。
可以简单地推导出一个递推表达式:
该表达式联系了前一时刻和后一时刻的回报
策略与价值函数
策略
在MDF中,从一个状态到一个动作的映射称为策略,分为确定性策略和 随机性策略
确定性策略
一个确定性的策略可以是 agent 会选择动作
随机性策略
使用
来描述策略
价值函数
在给定策略 状态价值函数 或者是 状态-动作价值函数
状态价值函数
状态价值函数定义为:
即在策略
状态-动作价值函数
状态-动作价值函数定义为:
其意义是很明确的。
Bellman Equation
状态价值函数的Bellman Equation
根据上面的那个递推表达式
这个式子其实是很自然的,就是先写成期望的形式,然后把最开始的回报展开一项,再把期望展开成所有可能的动作和之后的奖励及状态,再把后面的部分替换成下个状态的回报就可以了
状态-动作价值函数的Bellman Equation
同理可以推导出动作价值函数的Bellman Equation:
最优策略
注意到,各个策略之间可以找到一个偏序关系,即对于策略
记这个最优的策略为 最优价值函数 记为
同时还可以写出最优状态-动作价值函数:
两者之间的关系是
