齐次坐标系

参考文章：知乎

在二位笛卡尔坐标系中，一个点可以被表示为 而一条直线就是 但是此时有个问题，无法刻画两条平行线在无穷远处相交的情况，即对于透视空间无法处理，此时就需要引入齐次坐标系，在齐次坐标系中一个点被表示为 例如一个点 在齐次坐标系下的表示就是 而一旦这个点被平移到无穷远处那么在齐次坐标系下的表示就是 了。

齐次坐标系与笛卡尔坐标系的转换如下：

影像坐标系

参考文章：CSDN

在影像坐标系下面，有两套体系，一套是以像素为单位的 坐标系，另一套是以物理尺寸为单位 坐标系，如果我们知道了像主点的位置 那么这两个坐标系的转换关系如下：

这里的像主点就是摄影中心在图像上的投影点

相机坐标系(Camera)

三维相机坐标系和二位影像坐标系之间的对应关系是，相机坐标系的原点在摄影中心，相机坐标系的 轴和 轴分别与影像坐标系的 轴和 轴平行，而 轴垂直于像平面且朝向像平面，根据定义可以得知，此时的影像坐标系下面的所有点的 值都等于焦距 那么在影像 坐标系下面的点 在相机 坐标系下的坐标就是

根据中心投影的特征，假设像素点 是物理点的投影，那么摄影中心，像素点和物理点应该在同一条直线上面，所以满足方程：

可以写成矩阵的形式：

接下来带入上面 坐标系到 坐标系的转换，可以看到

那么这里面的 一般被称为尺度因子 而中间的那个 的矩阵被称为内参矩阵 ，那么更加简单的写法是

现实情况下，这个坐标系可能不是横平竖直的，可能是倾斜的，长下面这个样子：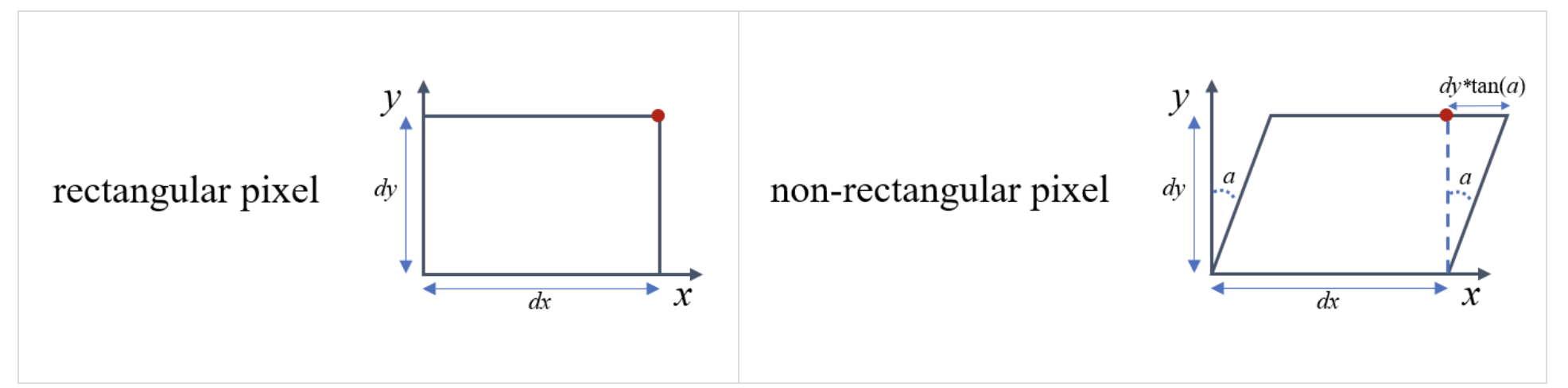

那么就需要在内参矩阵里面引入一个倾斜因子，此时的内参矩阵为：

这里的

所以最后到 坐标的转换就是：

世界坐标系

世界坐标系是以真实世界中的某个点作为原点，以真实世界的 作为朝向的坐标系，世界坐标系和相机坐标系都是三维坐标系，两者之间可以通过旋转-平移变换进行转换

定义一个三维的正交旋转矩阵 和一个平移矢量 ，那么把真实世界中某个点 转换成相机坐标系坐标 ：

或者写成另一种形式：

而把

称为相机的外参矩阵

如果在齐次坐标系下，这个外参矩阵可以写为一个方阵：

在齐次坐标系下，相机坐标系到世界坐标系的转换可以被写为：