论文原文

论文原文是20年的这一篇 Denoising diffusion probabilistic models 论文的地址： Arxiv.org

题外话，现在网上的教程都是一个抄一个，有个公式打错了结果我发现网上大部分教程都打错了 :-(

模型的整体思路

整体的流程润下图所示：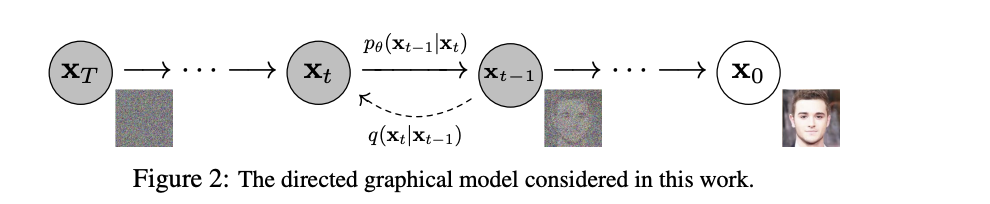

首先是从训练集开始不断地往上面加高斯噪声，最后直到达到一个纯随机的分布，再训练这个去除噪声的过程，从任意一个纯随机分布开始，一步步地去除噪声，直到还原出最后的图片

加噪声的过程

引理

考虑原输入和一个高斯噪声的加权平均的过程，假设第步时，原输入为加上了一个为的高斯噪声，对应的权重为和，其中的由于独立的高斯分布具有可加性，即满足那么考虑再往前一步的噪声有：

这其中的

考虑权重的一个前缀累乘，记有

注意到这里的的符号其实不重要，都是从中采样的随机高斯噪声，所以我们可以发现第步的分布本质上只由一系列的权重决定，这个式子更重要的是可以推导出下面的式子：

上面的式子

加噪声的过程

在论文中，加噪的过程被描述为：

如果你对这个式子里面的正态分布为什么有三个参数感到迷惑，你可以理解为第一个分号前面的是指明这个正态分布是描述变量的

那么考虑从最开始的图像加噪步得到的分布：

根据前面的引理，记可以得到：

去除噪声的过程

去除噪声的过程简言之就是推到出后验概率然后一步步地还原回去

已经有论文证明了在充分小的情况下，仍然满足正态分布，那么做出如下假设：

而这里面的和就是需要通过神经网络学习的均值参数和方差参数。

接下来考虑怎么去求一个loss，这样就可以优化这两个参数了，注意到如果知道可以计算：

这里面的是剩下的所有与无关的项

上面式子中的第一步是根据贝叶斯公式把先验概率转换成后验概率

第二个正比是因为这里已经全是后验概率了，全是高斯噪声，而高斯分布的计算公式是：

去掉第一项就是正比

由于我们知道这个分布是近似为正态分布的，那么把这个正态分布记为：

接下来求这两个参数和：
根据正态分布的表达式，有：

将之前得到的式子

带入上面求参数的式子可以得到：

在上面的式子中，只有第步噪声是不知道的，

另一篇博客的记号

加噪过程

记加噪过程为：

其中这里的接近与表示每一步对于分布的破坏情况

可以得到如下的算式：
$$
\begin{split}
x_t &= \alpha_{t} x_{t - 1} + \beta_t\epsilon_t\
&= \alpha_{t} (\alpha_{t - 1} x_{t - 2} + \beta_{t - 1}\epsilon_{t - 1}) + \beta_t\epsilon_t\
&= \cdots \
&= \prod_{i = 1}^T\alpha_i x_0 + (\alpha_t\cdots\alpha_2)\beta_1\epsilon_1 + (\alpha_t\cdots\alpha_3)\beta_2\epsilon_2 + \cdots +\alpha_t\beta_{t - 1}\epsilon_{t - 1} +\beta_{t}\epsilon_t\
&=\prod_{i = 1}^T\alpha_i x_0 + \sqrt{1 - \left(\prod_{i = 1}^T\alpha_i\right)^2}\bar{\epsilon}t,\bar{\epsilon}t \sim \mathcal N (0,I)
\end{split}
$$
这里记 $\bar\alpha_t = \prod{i = 1}^T\alpha_i $而$ \bar\beta_t = \sqrt{1 - \left(\prod{i = 1}^T\alpha_i\right)^2} $有$ $这里还应该注意到，如果不把后面的全部合并，可以留一项，变成：$ $

去噪过程

考虑重建的去噪过程，其实本质上就是在给定第步的分布时，如何更好地预测第步的分布

这里记为预测的第步的分布，那么可以自然地想到，一个使用欧氏距离的损失函数是：

由于我们注意到，这里面的可以写成

的形式，那么我们可以把这里的预测模型写成类似的形式：

这里面的其实就是在预测在分布下，这一步应该去除多少的噪声

带入计算，可以得到损失函数：

带入式中的可以得到：

这就是最后的损失函数了。

减少采样变量个数降低方差

观察上面的损失函数，这里面每一轮训练有四个东西需要采样：

:这是从样本里面采样一个图片出来
采样两个噪声出来
采样